Russian Federation
Russian Federation
Russian Federation
This paper discusses various aspects of the use of Carnot cards in the context of digital automata. Carnot maps are a special compact form of the truth table, which allows not only to represent a logical function, but also to minimize it.
Carnot cards, types of Carnot cards, basic principles of operation, digital automata, logical functions
В мире цифровых систем и программирования ключевую роль играют логические функции, которые позволяют моделировать и контролировать различные аспекты цифровых систем и программ, используя реальные значения. Однако по мере усложнения логических функций их становится все труднее анализировать и упрощать. В таких случаях они выступают в качестве мощного инструмента, способного упростить и объяснить логические функции.
Карты Карно придумал Эдвард В. Вейч в 1952 году. Физик Морис Карно улучшил их в 1953 году, позволяя нам эффективно упрощать и анализировать логические функции. Карты представляют функции в виде таблиц в двоичной системе счисления. Основная идея карты Карно состоит в том, чтобы представить любую возможную комбинацию значений входных переменных в виде ячейки таблицы, где соответствующие ячейки помечены значениями функций.
Карта Карно — это альтернативная форма представления таблицы истинности, она позволяет механизировать способ минимизации без применения алгебраических средств.
Существует несколько способов минимизации логических функций. Первый способ – арифметический: использование математических форм и различных законов, которые позволяют упростить ту или иную логическую функцию. Также наряду с этим существует и графический способ минимизации или упрощения логических функций. Это способ, который позволяет наглядно увидеть какие элементы формулы можно сократить
Карты Карно позволяют эффективно упрощать и анализировать логические функции. Они представляют функции в виде таблиц с использованием двоичной системы. Основная идея карты Карно состоит в том, чтобы представить любую возможную комбинацию значений входных переменных в виде ячейки таблицы со значениями функций, отмеченными в соответствующих ячейках.
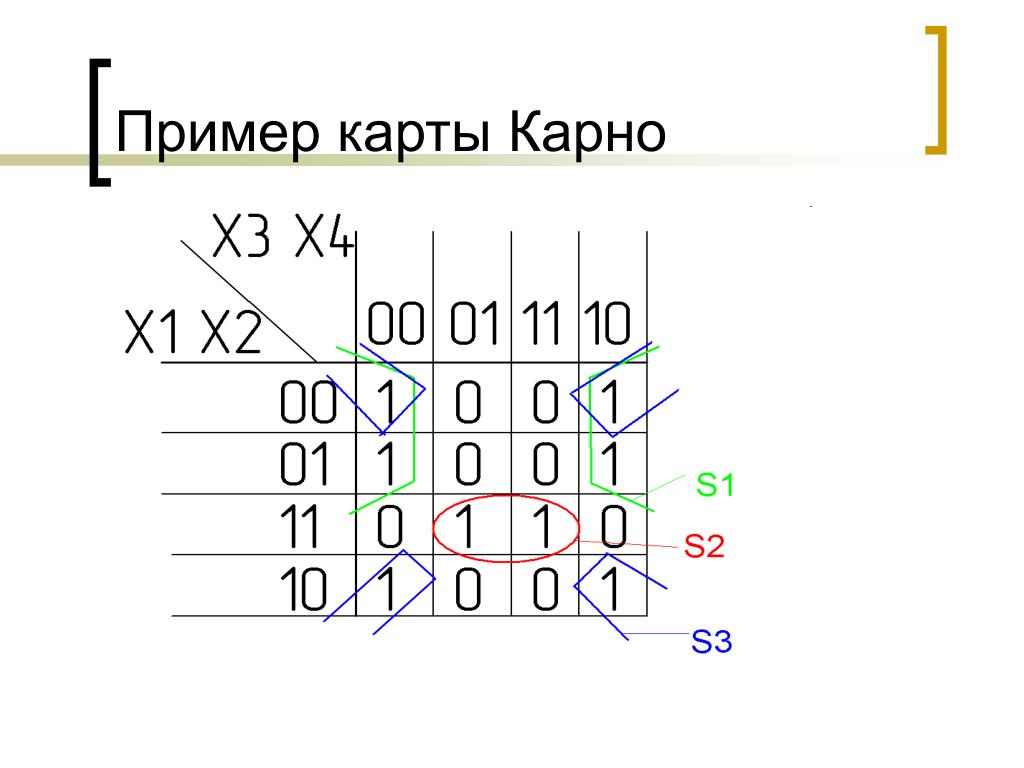
Рисунок 1 – Пример карты Карно
Для анализа функций с помощью карты Карно необходимо найти максимальное количество прямоугольников, содержащих значения 1. Каждый прямоугольник вложен параллельно по вертикальным или горизонтальным линиям таблицы и должен быть равен определенной степени. Эти прямоугольники можно использовать для выявления закономерностей в функции и упрощения ее выражения. Для двух переменных нам нужна карта, которая состоит из четырех клеток. То есть четыре элемента, которые находятся внутри.
Основная идея карт Карно – представление логических функций в виде таблицы, где каждая ячейка соответствует возможной комбинации значений входных переменных, а ячейки указывают значение функции. Для упрощения функций с использованием карт Карно используются шаблоны, помогающие уменьшить количество переменных и упростить выражение.
Существует два типа карт Карно: для логических функций с несколькими переменными и для функций с несколькими входами и выходами. Карты Карно для функций многомерной логики представляют собой прямоугольный массив, в котором каждая ячейка соответствует возможной комбинации значений входных переменных. Карта Карно для функций с несколькими входами и выходами представляет собой комбинацию нескольких карт Карно для логических функций с одной переменной.
Преимущества использования карт Карно включают интуитивно понятный и графический доступ к объектам. Они позволяют визуально распознавать узоры и рисунки, делая особенности более четкими. Карты Карно также помогают распознавать закономерности и упрощают логические функции, делая их более понятными и простыми для анализа. Они также помогают обнаруживать ошибки в логических функциях, например, чрезмерные или неправильные комбинации переменных.
Основным методом минимизации логических функций, заданных в совершенной дизъюнктивной нормальной форме или совершенной конъюнктивной нормальной форме, является операция неполного прилипания и элементарного поглощения. Операция попарной склейки выполняется между двумя термами (термами), содержащими одинаковые переменные, вхождения которых (прямые и обратные) одинаковы для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а прямые и обратные записи одной переменной, оставшейся в скобках, можно склеить вместе. Пример:

Возможность поглощения следует из очевидных равенств

Поэтому основная задача минимизации СДНФ и СКНФ состоит в том, чтобы найти подходящие условия для адгезии с последующейим поглощением, что может быть довольно сложной задачей для больших форм. Карты Карно предоставляют визуальный метод поиска этих данных.
Безусловным достоинством минимизации на единичном кубе является наглядность. Но очевидно, что даже если у нас всего лишь 4 переменных, мы сталкиваемся с затруднением, потому что изобразить четырехмерный единичный куб – задача не из легких. Нам на выручку приходит другой графический способ минимизации – карта Карно. По сути, карта Карно представляет из себя развертку n-мерного куба. И на практике применяется до случая, когда мы имеем до 6 переменных нашей функции. Итак, поскольку карта Карно является разверткой n-мерного куба, то должно выполняться то же самое условие для ячеек карты, как и для вершин нашего куба. То есть при переходе от ячейки к ячейке у нас меняется только одна переменная, а столбцы наши, по сути, записаны в виде кодов Грея.
Минимизация заключается в том, что мы должны покрыть наши карты Карно прямоугольниками, которые имеют стороны, равные некоторой степени двойке. Для слоя четырех переменных возможны 4 варианта – 2 прямоугольника из 2 кубиков и 2 прямоугольника из 4. При этом очень важно напомнить следующую вещь. Поскольку карта Карно – это развертка n-мерного куба, на самом деле она изображена у нас не на плоскости, а на торе. То есть считается, что верхняя строчка будет соседней с нижней строкой самый крайний левый столбец соседний с самым крайним правым столбцом.
На рис. 2 показаны простая таблица истинности для функции двух переменных, двумерный куб (квадрат), соответствующий этой таблице, а также двумерный куб, размеченный элементами СДНФ соответствующая таблица группировки выражений:

Рисунок 2 – Таблица истинности для функции из двух переменных
На рис. 3 в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующего ей куба.

Рисунок 3 - Таблица истинности для функции из трёх переменных
Основными принципами работы карт Карно в цифровых машинах являются представление логических функций в виде таблиц, их целенаправленный анализ и упрощение с помощью прямоугольников, а также использование графического подхода для обнаружения закономерностей. Карты Карно являются эффективным инструментом упрощения и анализа логических функций и широко используются в цифровых системах и программировании.
1. B.V. Cybakov «Sistemy avtomatizacii i upravleniya. Metodicheskie ukazaniya k raschetno-graficheskoy rabote», izd-vo AGTU, 2002g. - 67s.
2. A.Ya. Saveliev «Prikladnaya teoriya cifrovyh avtomatov», Moskva, izd-vo «Vysshaya shkola», 1987 g.
3. L.N. Prisnuhin, P.V. Nestrov - «Cifrovye vychislitel'nye mashiny», Moskva, izd-vo «Vysshaya shkola», 1981 g.
4. Solov'ev G.K. Arifmeticheskie ustroystva EVM. - M. “Energiya”. 1978.
5. Poluektov A.V., Makarenko F.V., Yagodkin A.S. Ispol'zovanie storonnih bibliotek pri napisanii programm dlya obrabotki statisticheskih dannyh // Modelirovanie sistem i processov. – 2022. – T. 15, № 2. – S. 33-41.




